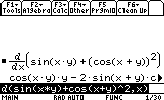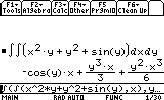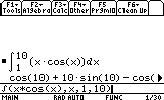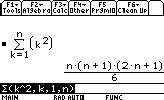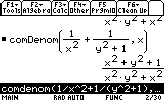Tutoriel TI-89
La TI-89 est une excellente calculatrice,c'est l'une des meilleures calculatrices actuellement (la HP-49G est aussi une bonne calculatrice , la TI-92 Plus a les mêmes fonctions que la TI-89 mais offre en plus des applications de Géométrie tel le logiciel Cabri Géomoètre et le logiciel "the Geometer's Sketchpad" ).
P.S:Ce tutoriel ne couvre pas toutes les fonctions présentes dans cette calculatrice (il y en a trop, pour cela consulter le manuel d'utilisation ).
|
Calculs simples |
Résoudre des équations et systèmes d'équations:
Supposons que l'on veuille résoudre l'équation suivante: -3x3 +3 x2 -2x+5=0
La syntaxe est:
|
Supposons vouloir résoudre le système d'équations suivant :2x-3y+5z=-1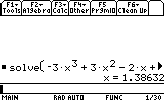
J'ai écris ",x" après l'équation car la variable dans cette équation est x
-3x+5y-2z=3
5x-7y+8z=-2
|
solve(2x+3y+5z=-1 and -3x+5y-2z=3 and 5x-7y+8z=-2,{x,y,z}) |
Dérivation et Intégration:
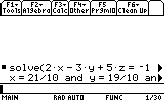
DérivationSupposons que l'on veuille trouver la dérivée de: x2+3x-5
La syntaxe est:
d(fonction,variable,degré)
degré est facultatif,,il est 1 par défaultIntégration:
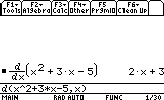
Calculer la dérivée partielle fx de: f(x)=sin(x*y) +cos2(x+y)
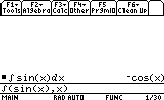
Caculons la primitive (intégrale) de sin(x):
Calculons : [x2 y + y2 +sin(y)] dxdy (on intègre pour x en supposant y constant puis we on intègre pour y en supposant x constant)
Calculons l'intégrale de x*cos(x) entre 1 et 10:
Limites,sommes et séries de Taylor
Limites
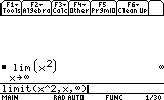
Calculons la limite de x2 quand x tend vers l'infini
La syntaxe est
lim(fonction,variable,point,direction)
direction est soit 1 soit -1
1:si c'est par valeurs positives (de la droite)
2:si c''est par valeurs négatives (de la gauche)direction peut être omis
Sommes:Somme de k2 avec k entre 1 et n
Séries de Taylor (Développement limité):
La syntaxe est :
Polynomes
taylor(fonction,variable,degré,point)
point peut être omis et est 0 par défaut
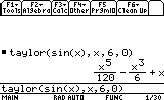
Calculons le développement limité de sin(x) autour de 0:
Développer des polynomesLa syntaxe:
expand(polynomial,variable)
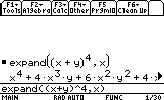
Factoriser des polynomes:Développons : (x + y)4
La syntax est::
Opérations sur les nombres:
factor(function,variable)
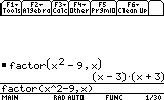
Factoriser: x2-9
- Réduire au même dénominator:
Réduire au même dénominateur la fonction suivante : (1/x2)+(1/(y2+1))
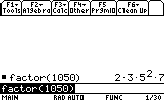
Factoriser un nombre:
|
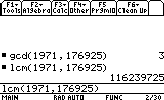
Trouver le PGCD(gcd) et le PPCM(lcm) de 2 nombres:Factorisons le nombre suivant: 1050
Equations différentielles
gcd(nombre1,nombre2)
lcm(nombre1,nombre2)
PGCD et PPCM de plusieurs nombres:
Trouvons le PGCD et le PPCM de 3 nombres:
gcd(gcd(nombre1,nombre2),nombre3)
lcm(lcm(nombre1,nombre2),nombre3)
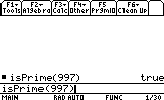
Testons si un nombre est premier ou pas:
isPrime(nombre)
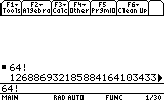
Calculer la factorielle d'un nombre:Testons si 997 est premier
Calculons :64!
SuitesRésolvons l'équation différentielle suivante: x''+w2x=0
deSolve(fonction,x,y)
On doit renommer x par y
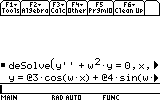
Notons que le résultat est : @3 cos (w.x)+@4 sin(w.x)
@3 and @4 sont des constantes
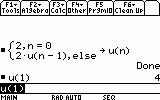
Supposons que l'on veuille trouver les termes de la suite suivante : Un+1=2*Un+2 avec U0=2
On peut utiliser deux méthodes: la fonction when ou bien en définissant une suite en mode Sequence de la calculatrice.
1. 1ère méthode: la fonction when:
- La syntaxe de la fonction when est:
when(condition,valeur vraie,valeur fausse,valeur inconnue)
valeur fausse et valeur inconnue peuvent être omis.
when(n=0,2,2*u(n-1)+2) ->u(n)
le signe " -> " est pour sauvegarder la fonction dans u(n)
Pour calculer u1on écrit : u(1)
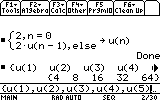
Supposons que l'on veuille les 5 premiers termes de cette suite, on écrit:
{u(1),u(2),u(3),u(4),u(5)}
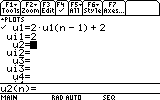
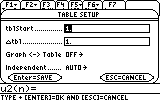
- 2. A partir du mode Sequence:
Prenons l'exemple précédent:
La syntaxe est:
u1=2*u1(n-1)+2
ui1=2
ui1 est le terme initial
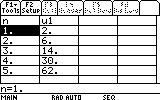
Notez que la table commence a 1 donc en fait u0 est égal à n=1 sur la calculatrice,il y a donc un décalage de 1